一、死循环法

#include<stdio.h>
int main(){
int m;
int n;
scanf("%d %d",&m,&n);
int gcd = m > n ? n : m;
while(1){
    if(m%gcd==0 && n%gcd==0){
        printf("%d",gcd);
        break;
    }
    else{
        gcd--;
    }
}
 int lcm = m*n/gcd;
    printf(" %d\n",lcm);
 return 0;
}

循环次数过多超时，int最大数据是2^9 这里如果m和n中最小的数为2^9,则需要循环2^9次，计算机1s一般可以循环2^8次，这里要求400ms，所以超时。

二、暴力转除法

#include<stdio.h>
long long a,b;
long long isp(long long x){
for(long long i=2;i*i<=x;i++){
    if(x%i==0) return 0;//不是质数
}
return 1;//质数

}//isp是判断是否为质数的函数

long long f(long long a,long long b,long long na,long long nb,long long i){
if(na>nb){
    long long t=na;
    na=nb;
    nb=t;
}//交换值操作，是为保障后面的nb%na一定是大的除以小的；
if(isp(na)){
    if(nb%na==0) return na;
    else return 1;
}//不是质数的情况下，若nb能整除na 那na是na和nb的最大公约数；
if(i*i>na||i*i>nb) return 1;//但满足前面条件，i从此以后不再可能是他俩公约数；return1 相当于没乘；
long long res=1;
if(isp(i)){
    while(na%i==0) na/=i;
    while(nb%i==0) nb/=i;
    long long pow=0;
    while((a%i==0)&&(b%i==0)){
        a/=i;
        b/=i;
        pow++;
    }//这个while语句是用来判断a，b里面最多公有多少个质因数i 用pow表示;
    while(pow--) res*=i;//这样可以得到i^pow;
}//这里if语句判断i是否为质数，是为了保证除以的是质因数;
return res*f(a,b,na,nb,i+1);//递归;
}
int main(){
scanf("%lld %lld",&a,&b);
long long gcd=f(a,b,a,b,2);
printf("%lld %lld",gcd,a*b/gcd);//最大公约数*最小公倍数 = a * b；
return 0;
}

模拟转除，但自定义函数较繁琐；

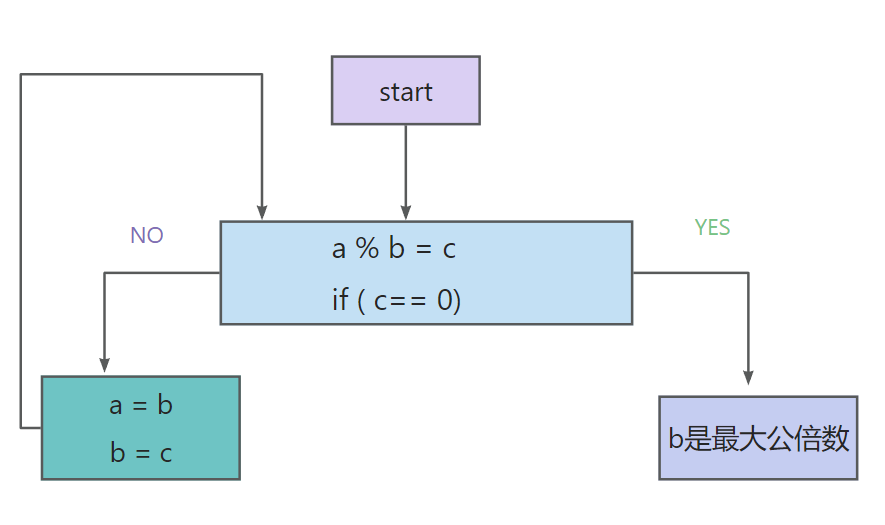
三*、辗转相除法（Euclidean algorithm）

#include<stdio.h>
int main()
{
int a = 0;
int b = 0;
scanf("%d %d", &a, &b);
while (1)
{
    int c = a % b;
    if (0 == a % b)
    {
        printf("%d就是最大公约数", b);
        break;
    }
    else
    {
        a = b ; 
        b = c;
    }
}
return 0;
}